Operações elementares
O conjunto dos números complexos é um corpo. Portanto, é fechado sobre as operações de adição e multiplicação, além de possuir a propriedade de que todo elemento não-nulo do conjunto possui um inverso multiplicativo. Todas as operações do corpo podem ser performadas através das propriedades associativa, comutativa e distributiva, levando em consideração a identidade
Sejam z e w dois números complexos dados por
 e
e  então definem-se as relações e operações elementares tal como segue:
então definem-se as relações e operações elementares tal como segue:- Identidade:
 se e somente se
se e somente se  e
e 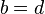 .
.
- Soma:
- Produto:
- Conjugado:
Exemplo número complexo com módulo 2 e argumento 120°. Em vermelho o conjugado deste número em em verde o oposto.
 , onde
, onde  denota o conjugado de z. Outra notação usada para o conjugado de
denota o conjugado de z. Outra notação usada para o conjugado de  é
é 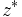 .
.
- Soma de um Complexo por seu Conjugado:
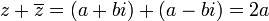 .
.
- Produto de um Complexo por seu Conjugado:
 .
.
Como , temos que o produto de um Número Complexo
, temos que o produto de um Número Complexo 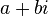 pelo seu Conjugado
pelo seu Conjugado 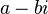 se dá por:
se dá por:  .
.
- Módulo:
- Inverso multiplicativo (para
 ):
):
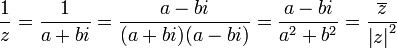 .
.
As operações de subtração e divisão são efetuadas transformando em adição com o oposto aditivo e em multiplicação com o inverso multiplicativo, respectivamente. Algumas operações são mais facilmente realizadas na forma polar: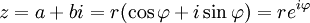 .
.
- Produto:
- Inverso multiplicativo (para
 ):
):
- Divisão:
- Potenciação:
- Conjugado:
O módulo
Sejam z e w dois números complexos dados por e
e  , o módulo possui as seguintes propriedades:
, o módulo possui as seguintes propriedades:definida como:
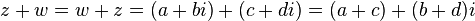

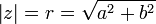
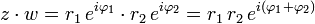
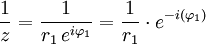
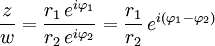


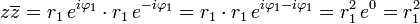


Nenhum comentário:
Postar um comentário